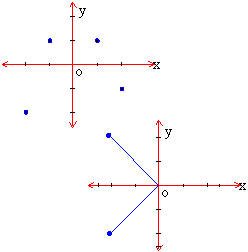
Example A relation is given as { ( 1, 1 ), ( 2, 1/2 ), ( 3, 1/3 ), ( 4, 1/4 ) } is it a function ? Justify. If yes, then state its domain and range. Exhibit the relation by a formula.

Solution : Let A = { 1, 2, 3, 4 } and B = { 1, 1/2 , 1/3, 1/4 }. Every element in A occurs once and only once in the ordered pairs and related to one and only one element of set B, exhibiting a relation. Hence it is a function from set A to set B. Let it be 'f ' then,

Range of 'f ' = set B = { 1, 1/2 , 1/3, 1/4 }

Also the second member of each ordered pair is the reciprocal of its first member. If we denote member of A as x and that of B by y then,

y = 1/x Þ f ( x ) = 1/x x Î A

Example Observe the following graphs. Determine whether the relations are functions or not. If so, state their domain and range.

Solution : Function : Yes (1)

Domain = { -2, -1, 1, 2 }

Range = { -2, 1, 1, -1 }

Domain = { x | -2 £ x £ 0 } (2)

Range = { y | -2.5 £ y £ 2.5 }

No, it is not a function.

Solution : Since 'f ' is a real valued function