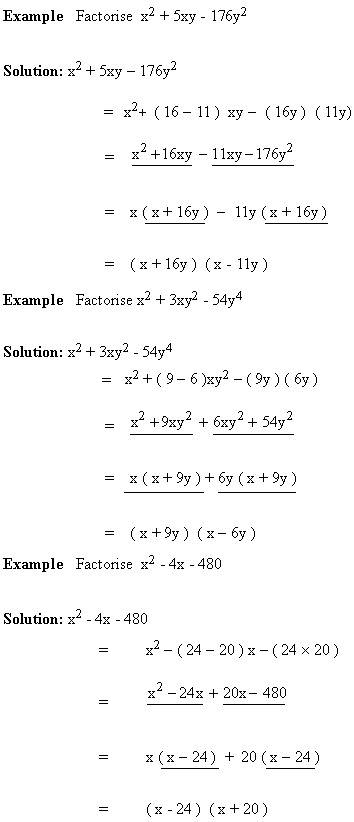
7. Factors of expressions of the form px² + qx + r and px² - qx + r.

If p, q, r stand for positive given numbers to factorise expressions of the form px² + qx + r and px² - qx + r , we have to replace q by the sum of two numbers whose product is p ´ r and sum is q and then proceed by grouping the terms.

Example Factorise 2x² + 11x + 15

Solution: Here 2 ´ 15 = 30 ; hence we need to find two numbers whose product is 30 and sum is 11. They are 6 and 5.

Therefore, 2x² + 11x + 15 = 2x² + ( 6 + 5 )x + 15

Example Resolve into factors 4x² - 19x + 15

Solution: Here 4 ´ 15 = 60. We hunt for two numbers whose product is 60 and sum is 19. They are 15 and 4.

Therefore, 4x² - 19x + 15 = 4x² - (15 + 4 ) x + 15

Example Factorize 8x² + 26x + 21

Solution: 8 ´ 21 = 168. We need to find two numbers whose product is 168 and sum is 26. The hunt for the two numbers id done this way.

Note 8 has factors : ( 4, 2 ), ( 2, 4), ( 8, 1), ( 1,8 ).

and 21 has factors: (21, 1 ), ( 1, 21 ) ( 3,7 ), ( 7,3 ).

[next page]

Index

3.1 - Introduction
3.2 - Monomial, Polynomials
3.3 - H.C.F and L.C.M

Chapter 4